PHP递归怎么用？关键点有哪些？-建站教程-锦华智联科技

什么是递归？ (核心思想)
递归的两大核心要素 (必须理解)
递归的基本结构 (代码模板)
递归实战案例 (从简单到复杂)
- 案例1：计算阶乘
- 案例2：斐波那契数列
- 案例3：遍历文件夹
递归 vs. 循环 (如何选择)
递归的优缺点与注意事项
- 优点
- 缺点
- 重要警告：栈溢出

什么是递归？

递归是一种在函数内部调用函数自身的编程技巧，你可以把它想象成一个“俄罗斯套娃”或者“照镜子”：

（图片来源网络，侵删）

俄罗斯套娃：你打开一个大的娃娃，里面有一个稍小的娃娃；你打开那个小的，里面还有一个更小的……这个过程不断重复，直到你打开最后一个最小的、没有其他娃娃的娃娃为止。
照镜子：你拿着一面镜子照自己，镜子里有你的影像；如果那面镜子后面还有一面镜子，你就会看到影像的影像,一层层嵌套下去。

在编程中，递归就是将一个复杂的问题分解成一个或多个与原问题相似但规模更小的子问题，直到子问题简单到可以直接解决，将子问题的解合并,得到原问题的解。

递归的两大核心要素

任何一个有效的递归函数都必须包含以下两个关键部分,缺一不可：

a. 基线条件 / 递归出口

这是递归的终止条件，它定义了递归应该在何时停止，如果没有基线条件，函数会无限地调用自己，最终导致栈溢出错误,程序崩溃。

好比俄罗斯套娃：最小的那个没有套娃的娃娃就是基线条件。
好比照镜子：最后一面镜子后面没有镜子了,就是基线条件。

b. 递归条件

这是函数调用自身的部分，它负责将问题规模缩小,并向基线条件靠近。

（图片来源网络，侵删）

好比俄罗斯套娃：每次打开一个娃娃，取出里面的那个稍小的娃娃,就是递归条件。
好比照镜子：每次你看到的影像中的镜子,都是递归条件。

递归的基本结构

记住这个通用的代码模板,你就能写出大部分递归函数。

function myRecursiveFunction($parameter) {
    // 1. 基线条件：检查是否已经到达可以停止递归的点
    if (isBaseCase($parameter)) {
        return simpleAnswer(); // 返回一个简单的、直接的答案
    }
    // 2. 递归条件：处理当前问题，并调用自身来处理更小的问题
    $smallerProblem = makeProblemSmaller($parameter);
    $result = myRecursiveFunction($smallerProblem); // 调用自身
    // 3. 合并结果：将子问题的解与当前问题的解合并
    return combineResults($parameter, $result);
}

流程总结：

检查基线条件。
如果满足,返回最终结果。
如果不满足，进行一些计算，然后调用自身，传入一个“更小”的参数。
等待子问题的返回结果。
将子问题的结果与当前的计算结合,返回给上一级调用。

递归实战案例

让我们通过几个经典的例子来理解递归的实际应用。

案例1：计算阶乘

问题：计算一个正整数 n 的阶乘（n!）。数学定义：n! = n * (n-1) * (n-2) * ... * 1 递归定义：n! = n * (n-1)!，且 1! = 1 (基线条件)

分析：

基线条件：当 n 等于 1 时，直接返回 1。
递归条件：n * factorial(n - 1)。

代码实现：

<?php
function factorial($n) {
    // 1. 基线条件
    if ($n == 1) {
        return 1;
    }
    // 2. 递归条件
    // $n * (n-1)的阶乘
    return $n * factorial($n - 1);
}
// 测试
echo "5的阶乘是: " . factorial(5); // 输出: 5的阶乘是: 120
?>

执行过程解析 (factorial(3))：

factorial(3) 被调用。3 不等于 1，所以执行 return 3 * factorial(2)。
- 程序暂停，等待 factorial(2) 的结果。
factorial(2) 被调用。2 不等于 1，所以执行 return 2 * factorial(1)。
- 程序暂停，等待 factorial(1) 的结果。
factorial(1) 被调用。1 等于 1，满足基线条件，直接返回 1。
回到第2步，factorial(2) 得到了 factorial(1) 的结果 1，它计算 2 * 1，并返回 2。
回到第1步，factorial(3) 得到了 factorial(2) 的结果 2，它计算 3 * 2，并返回 6。
factorial(3) 的调用返回 6。

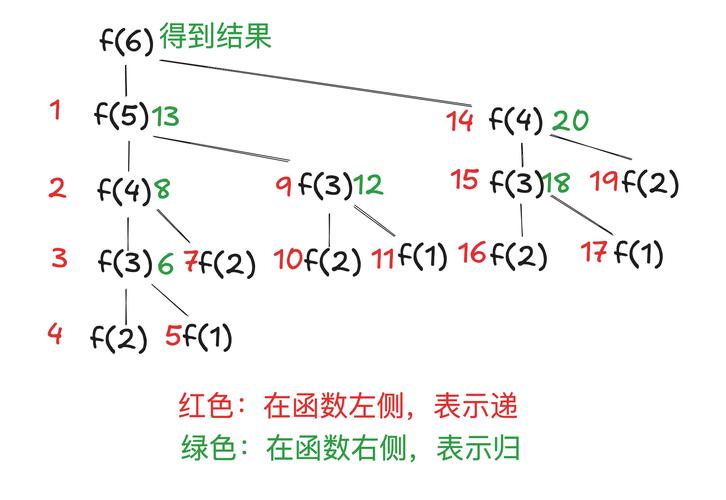
案例2：斐波那契数列

问题：斐波那契数列定义如下：F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2) (当 n > 1 时)。

分析：

基线条件：当 n 等于 0 或 1 时，直接返回 n。
递归条件：fibonacci($n - 1) + fibonacci($n - 2)。

代码实现：

<?php
function fibonacci($n) {
    // 1. 基线条件
    if ($n <= 1) {
        return $n;
    }
    // 2. 递归条件
    return fibonacci($n - 1) + fibonacci($n - 2);
}
// 测试
echo "斐波那契数列的第10项是: " . fibonacci(10); // 输出: 55
?>

注意：这个简单的斐波那契递归实现效率非常低，因为它会重复计算很多值（fibonacci(5) 会被计算多次），在实际应用中，对于斐波那契问题，使用循环或带有记忆化（Memoization）的递归会更高效。

案例3：遍历文件夹 (非常实用的例子)

问题：递归地列出某个目录及其所有子目录下的所有文件。

分析：

基线条件：当遍历到一个文件时,直接输出文件名。
递归条件：当遍历到一个目录时，获取该目录下的所有条目,并对每个条目再次调用遍历函数。

代码实现：

<?php
function listDirectory($path) {
    // 1. 检查路径是否存在且是一个目录
    if (!is_dir($path)) {
        echo "错误: $path 不是一个有效的目录。<br>";
        return;
    }
    // 打开目录句柄
    $items = scandir($path);
    if ($items === false) {
        echo "无法打开目录: $path<br>";
        return;
    }
    foreach ($items as $item) {
        // 跳过 '.' 和 '..'
        if ($item == '.' || $item == '..') {
            continue;
        }
        $fullPath = $path . DIRECTORY_SEPARATOR . $item;
        // 2. 如果是目录，递归调用
        if (is_dir($fullPath)) {
            echo "[目录] $fullPath<br>";
            listDirectory($fullPath); // 递归调用
        } else {
            // 3. 如果是文件，打印文件名 (基线条件的一种表现)
            echo "[文件] $fullPath<br>";
        }
    }
}
// 测试 (请将 'your_directory_path' 替换为你的实际目录)
// listDirectory('/path/to/your/directory'); // listDirectory(__DIR__);
?>

这个例子完美地展示了递归在处理树形结构数据（如文件系统、HTML DOM 树、组织架构图）时的强大能力。

递归 vs. 循环

特性	递归	循环
代码可读性	对于某些问题（如树形结构）非常清晰、优雅。	逻辑直接，但可能需要更多状态变量来跟踪进度。
性能	通常较慢，每次函数调用都有开销（创建栈帧、传递参数等）。	通常更快，没有函数调用的额外开销。
内存使用	较高，每次递归调用都会在调用栈上占用内存，深度过大时可能导致栈溢出。	较低，通常只使用固定数量的内存。
适用场景	问题本身具有天然的递归结构（如树、分形）。	简单的重复性任务（如遍历数组、累加求和）。

选择建议：

优先使用循环：对于简单的、线性的任务，循环是更安全、更高效的选择。
考虑递归：当问题的定义本身就是递归的，并且问题的深度不会太大时，递归能让代码更简洁、更易于理解。

递归的优缺点与注意事项

优点

代码简洁优雅：对于某些问题,递归可以用更少的代码表达复杂的逻辑。
自然贴合问题模型：当问题本身是递归定义时（如树、分形）,用递归实现是最直观的。

缺点

性能开销：函数调用比循环迭代慢。
内存消耗大：容易达到调用栈的深度限制。
调试困难：调用栈多层嵌套,错误追踪比较麻烦。

重要警告：栈溢出

这是递归最常见也最危险的陷阱。

原因：每次函数调用，系统都会在内存的调用栈上分配一个“栈帧”来存储函数的参数、局部变量和返回地址，递归函数不断调用自己，就会在栈上不断添加新的栈帧，如果递归深度过大（计算 factorial(100000)），栈的内存空间会被耗尽，程序就会崩溃并报错：Fatal error: Maximum function nesting level of '256' reached... (这个值可以在 php.ini 中修改 xdebug.max_nesting_level)。

如何避免？

确保有正确的基线条件：这是防止无限递归的根本。
评估问题深度：对于可能很深的递归（如遍历一个非常深的文件目录），要考虑改用循环或迭代方法，或者使用尾递归优化（但请注意，PHP 默认不支持尾递归优化，所以这个方法在 PHP 中基本无效）。

递归是一个强大而优美的编程工具,但它也是一把双刃剑。

核心思想：函数调用自身,将大问题分解为小问题。
两大要素：基线条件（停止点）和 递归条件（调用自身）。
关键结构：先判断基线，再递归调用,最后合并结果。
适用场景：天然具有递归结构的问题（如树、分形）。
致命风险：栈溢出,必须通过正确的基线条件来规避。

学习递归最好的方法就是多练习，从阶乘、斐波那契等经典问题开始，然后尝试解决更复杂的树形结构问题，理解了它的原理，你就能在合适的场景下,写出既高效又优雅的代码。